Gravitational Chaos
The Gravitational Three-Body Problem
The three-body problem in gravity can have chaotic solutions, which means that over time the solutions evolve in seemingly random and unpredictable ways. The gravitational equations of motion are completely deterministic, but the apparent random behavior arises from small—even imperceptible—differences in initial conditions that grow exponentially in time.
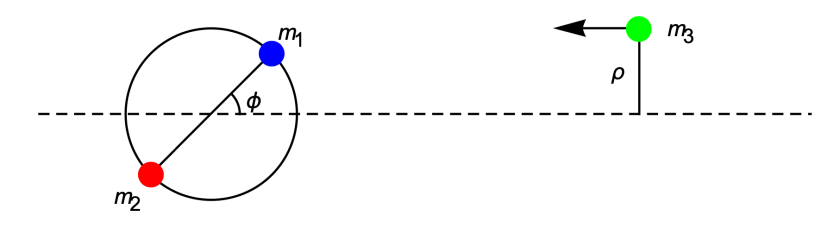
Chaos in General Relativity
As an example of chaos in gravity, consider a circular binary (red and blue masses in the figure above) that interacts with a third body (green mass) that travels along a straight line from infinity. A series of simulations are run with initial data characterized by the orbital phase (ϕ) and the impact parameter (ρ). The total energy of the system is positive, so that at least one body is ejected from the system. The pixels in the figures below show the color of the ejected body for Newtonian gravity (PN0), and different orders of the post-Newtonian approximation (PN1, PN2, and PN2.5). If the separation between two bodies becomes smaller than the sum of their Schwarzschild radii, then a collision takes place, and the pixel is colored black.
If we zoom into each of these figures, we see the complicated structure of these plots, typical of chaotic systems.

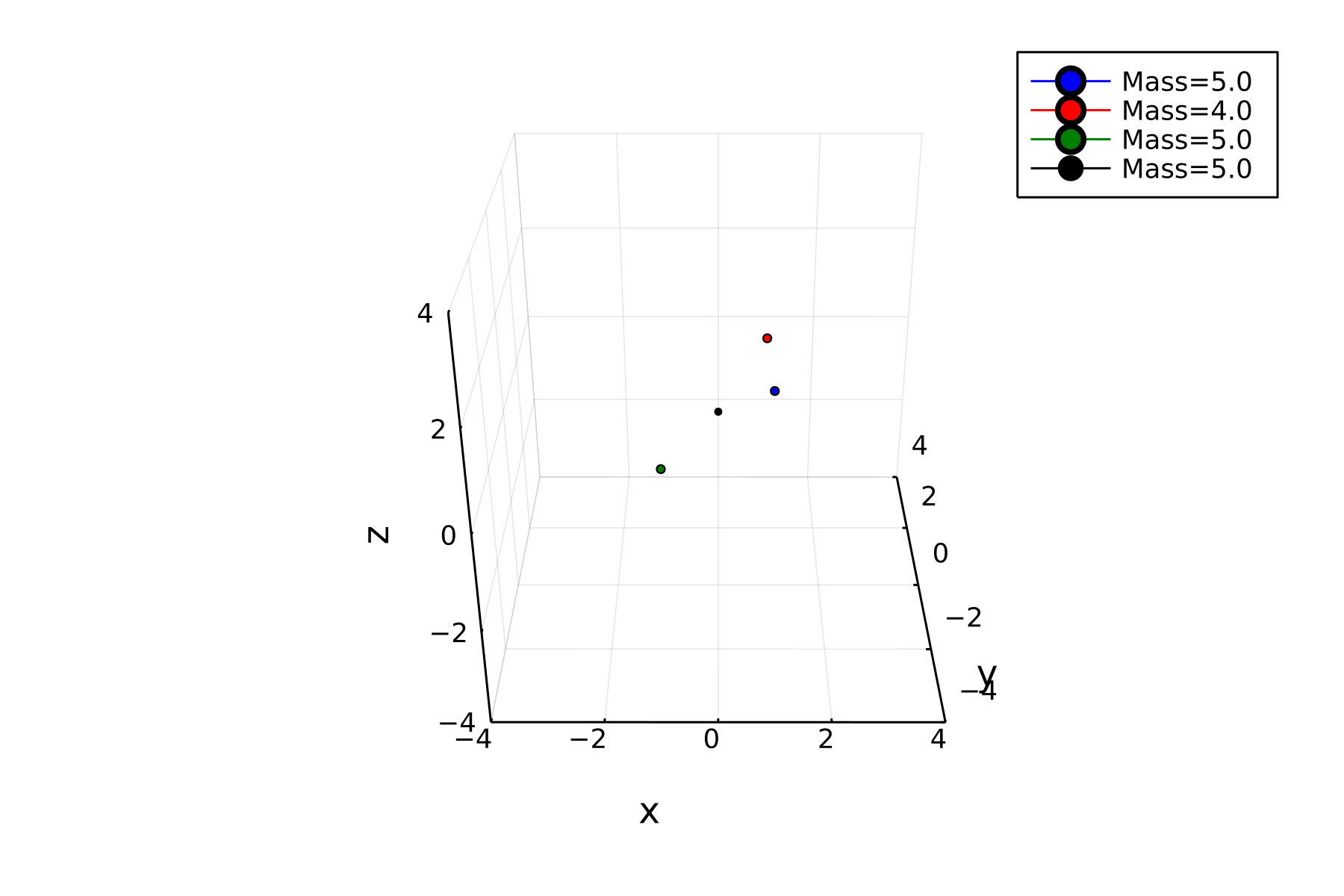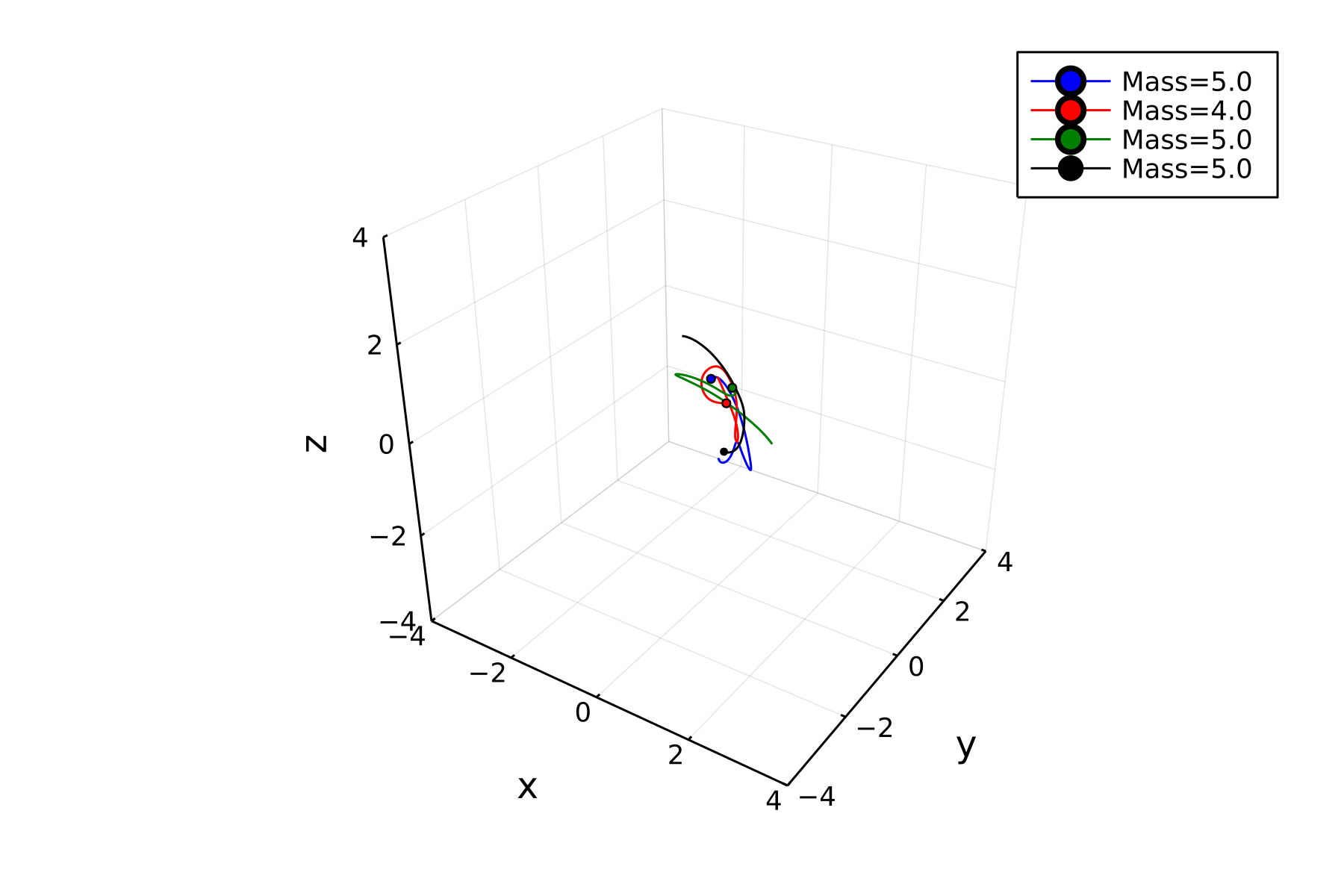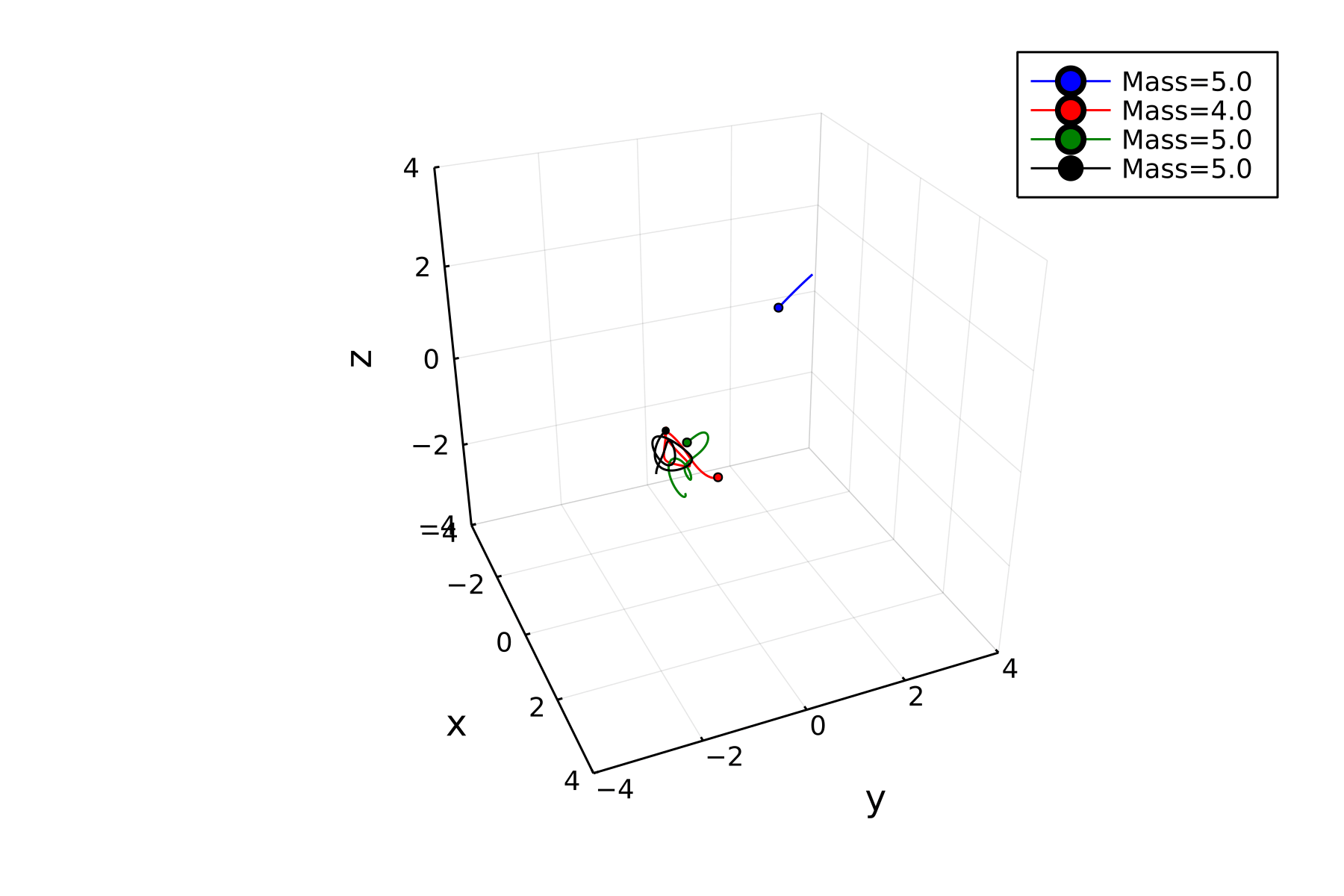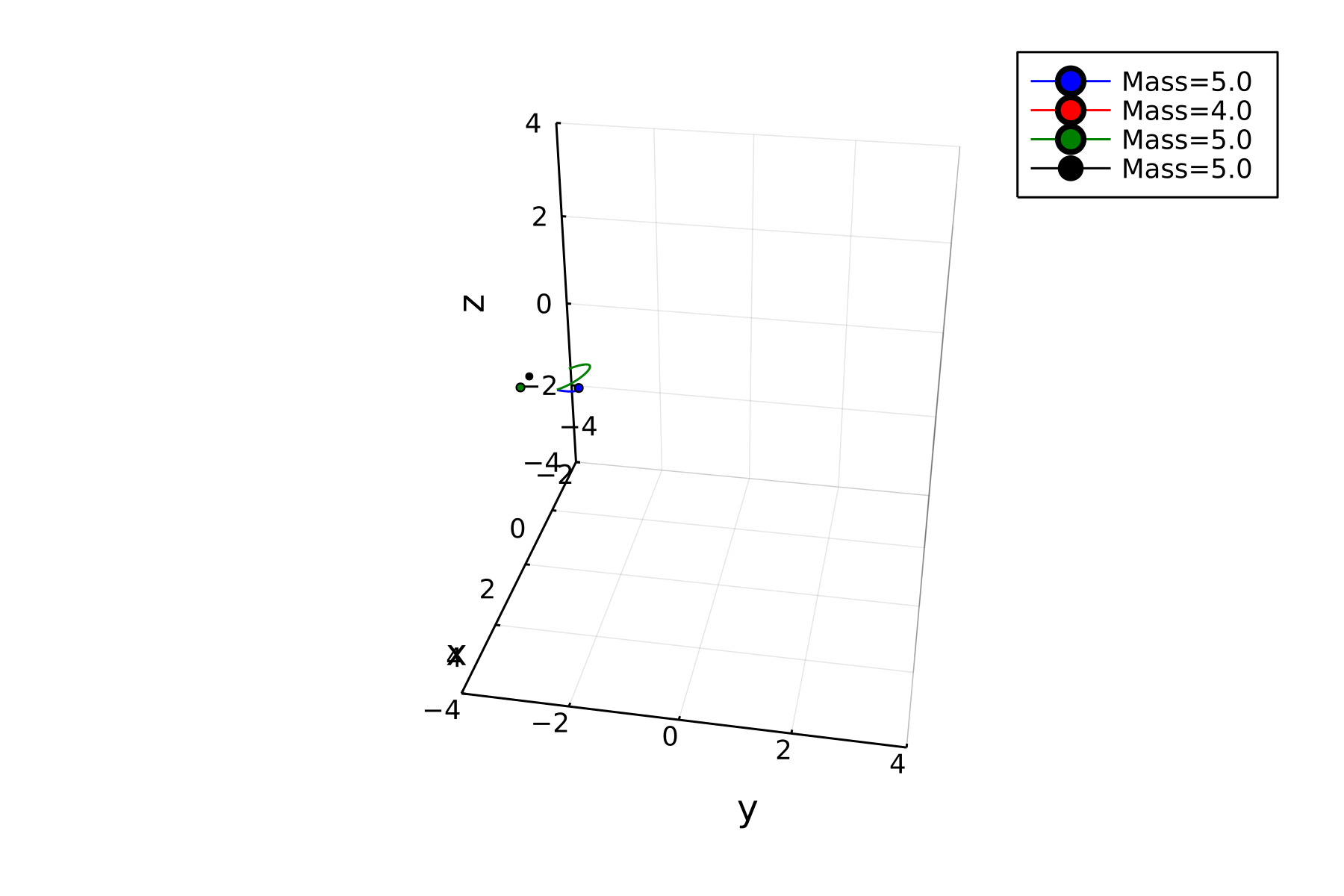
Many-Body Problem in Newtonian Gravity
The two-body problem in Newtonian gravity can be solved analytically, and the orbits are conic sections, either an ellipse (bound orbits), a hyperbola (unbound), or a parabola. For more than two bodies, however, the solutions can be much more complicated. For example, bodies that are initially bound may become unbound, as energy and angular momentum are transferred from one body to another. These movies show different many-body systems evolved with Newtonian gravity.
more text



