Wavelet Adaptive Multi-Resolution

Adaptive grids are important in many computational problems. Wavelet Adaptive Multi-Resolution (WAMR) uses the expansion of functions in a wavelet basis to generate the unstructured computational grid. Dendro-GR uses WAMR in simulations of binary black holes.

WAMR and Relativistic Fluids

The Riemann problem in fluid dynamics is a solution for the evolution of two discontinuous states. The solution has two waves, which can be either shocks or rarefaction waves. The plots below show a solution with a rarefaction wave (moving left) and a shock (moving right) at a fixed time. The top row shows the fluid density (ρ) and velocity (v), and the bottom left frame shows the pressure (P). The bottom right frame shows all of the points used to calculate the solution, with the vertical axis showing the different grid levels. The wavelet algorithm refines on non-smooth features of the solution, such as the shock and contact discontinuities, as well as the left and right end-points of the rarefaction wave.

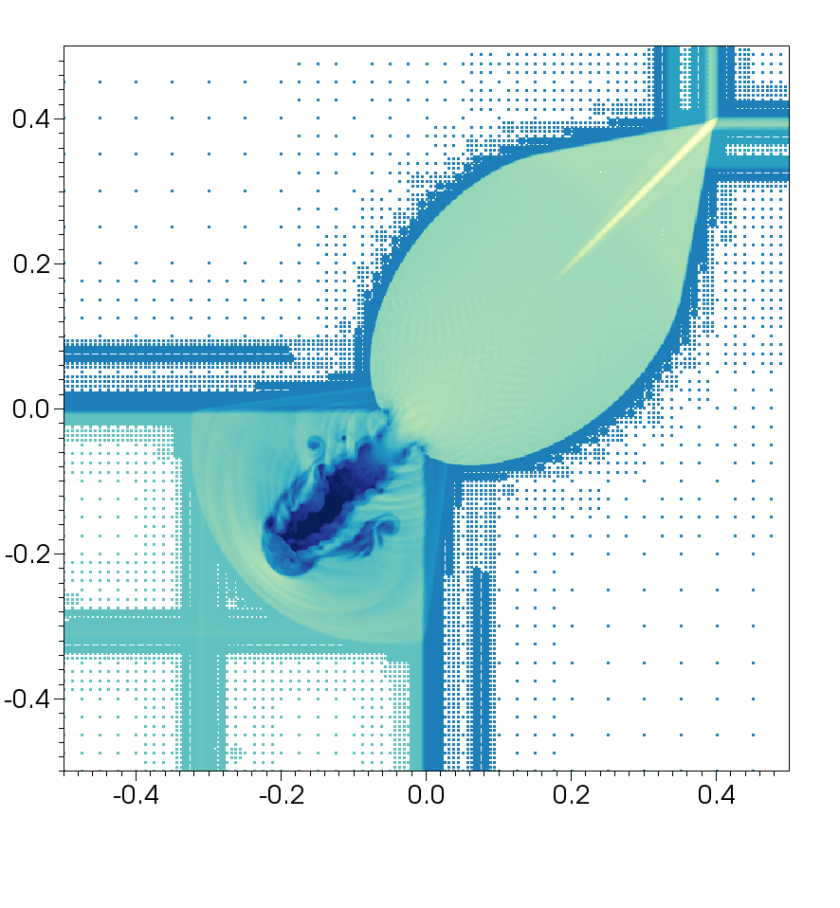
This figure shows the points used to calculate a Riemann problem in two dimensions with a bow shock.

The Non-Linear Sigma Model

A simple example for Dendro and WAMR is a wave equation with a non-linear potential, such as the non-linear sigma model [1]. This movie shows an evolution of two interacting pulses.

nlsmB.mp4

References:

1. Steven L. Liebling, "Singularity threshold of the nonlinear sigma model using 3D adaptive mesh refinement," Phys. Rev. D 66, 041703 (2002). DOI